Tree
In this unit Let me briefly tell you why we are studying this ADT
As you know that Searching an element using in a linked list takes ~0(n) time. How?
Let's assume that you wish to search an element named "A" in a given linked list ( Obviously LL is a data Structure) that contains elements A,B,D,E . What will be the worst case ( This is when The Element is placed at the last in the linked list) so how much time it will take to search this A now, Obviously you have to traverse each element and then you will be able to find A ., How many elements are there in the list ? 4 here , so if elements are n then how much time you will take in worst case = ~0(n). Fine!
Now if we can reduce this time to some Log time Don't you think it is more wonderful ?
How, Lets use the concept of one more non linear ADT called Trees. A tree is a non linear structure in which each node is connected with some other node (forming parent child relationship) to form a hierarchical structure. the point is to reduce the searching time !
But even before that lets try to understand different types of trees with their terminologies !
Now Hope you understood The definition ! Please keep in mind that some books follow slightly different conventions while defining the types of trees.
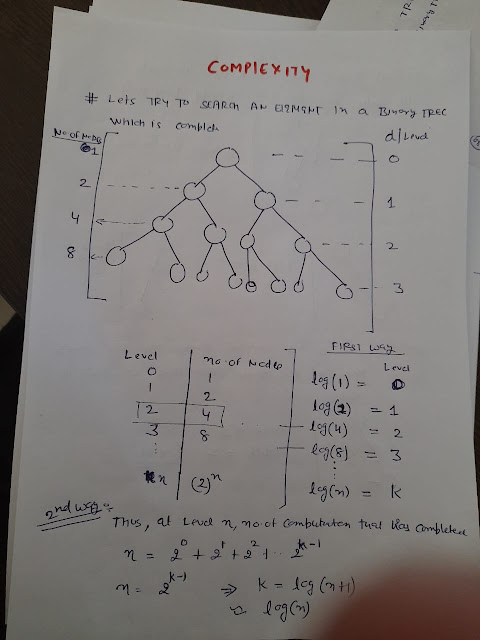
Now lets try to explore why the complexity turns out to be logn in searching for an element
In this unit Let me briefly tell you why we are studying this ADT
As you know that Searching an element using in a linked list takes ~0(n) time. How?
Let's assume that you wish to search an element named "A" in a given linked list ( Obviously LL is a data Structure) that contains elements A,B,D,E . What will be the worst case ( This is when The Element is placed at the last in the linked list) so how much time it will take to search this A now, Obviously you have to traverse each element and then you will be able to find A ., How many elements are there in the list ? 4 here , so if elements are n then how much time you will take in worst case = ~0(n). Fine!
Now if we can reduce this time to some Log time Don't you think it is more wonderful ?
How, Lets use the concept of one more non linear ADT called Trees. A tree is a non linear structure in which each node is connected with some other node (forming parent child relationship) to form a hierarchical structure. the point is to reduce the searching time !
But even before that lets try to understand different types of trees with their terminologies !
- We have discussed linear data structures, such as, Arrays, Strings, Stacks, and Queues.
- Now, we will learn about a Non-Linear Data Structure called TREE.
- A tree is a structure which is mainly used to store data that is hierarchical in nature. First, we will understand general trees and then Binary Trees.
- These binary trees are used to form binary search trees and heaps. They are widely used to manipulate Arithmetic Expressions, Construct Symbol Tables, and for Syntax Analysis.
Now Hope you understood The definition ! Please keep in mind that some books follow slightly different conventions while defining the types of trees.
Now lets try to explore why the complexity turns out to be logn in searching for an element
A) Best Time complexity - element is present at root = O(1)
B) Average Time Complexity in BST
There n is number of nodes in binary tree, if suppose you have n= 8 , then log(8)= 3 , i.e you need to process 3 levels in order to find any element.
But ! wait what if the tree is skewed !
C) And worst-case complexity is when tree is skewed
So, What will be the advantage of using trees if their complexity turns out to be ~0(n); Yes you are right there is no advantage if the tree is skewed but if it is complete or almost complete than you can take logn time advantage over ~o(n). Ok!
Hope You are now clear about the different terminologies used in Trees ! and the reason we are using this ADT
But wait I know that you reduced the time by using Trees but it is on the cost of inserting and deletion ! in Trees both operation involves traversing a node and then deletion/insertion. So in the worst case, A node is present at last and thus you need to traverse all the nodes in order to reach that node.
If visiting a node takes a C amount then to visit n nodes will take ~=Cx o(n) =O()n
Conclusion - Trees reduces searching (log (n) , in linked list = O(n)) but insertion and deletion time increases that is = O(n) which is O(1) in case of lionked list.
C) And worst-case complexity is when tree is skewed
So, What will be the advantage of using trees if their complexity turns out to be ~0(n); Yes you are right there is no advantage if the tree is skewed but if it is complete or almost complete than you can take logn time advantage over ~o(n). Ok!
Hope You are now clear about the different terminologies used in Trees ! and the reason we are using this ADT
But wait I know that you reduced the time by using Trees but it is on the cost of inserting and deletion ! in Trees both operation involves traversing a node and then deletion/insertion. So in the worst case, A node is present at last and thus you need to traverse all the nodes in order to reach that node.
If visiting a node takes a C amount then to visit n nodes will take ~=Cx o(n) =O()n
Conclusion - Trees reduces searching (log (n) , in linked list = O(n)) but insertion and deletion time increases that is = O(n) which is O(1) in case of lionked list.











No comments:
Post a Comment